Figure 1 – the “Golden Rectangle,” from the Wikicommons and in the public domain

As I indicated the “golden rule of thirds” is an approximation of the “golden proportion” aka the “golden ratio.”  The “golden proportion” comes from the ancient Greeks, so it must be cool and mystical.  But what exactly is it?

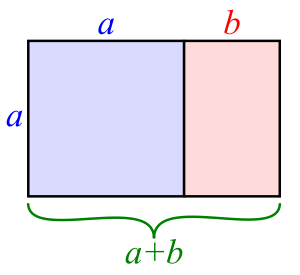
It is a special rectangle as shown in Figure 1.  The rectangle has a height, which we will call a and a width, which we will call a+b.  Now honestly that is true of all rectangles.  Since as long as the rectangle isn’t a square, the width is always a bit larger than the height.  So we might as well call that amount b.  But the “golden rectangle” has the special property that

(a+b)/a = a/b =ϕ

I know that a lot of you don’t like equations, but forget the equation.  All that I am saying is that for this particular rectangle, when I divide it as shown, I create a second rectangle only on its side, and that the width divided by the height is the same for both rectangles.  This ratio is so important that we’ve given it a name, really a symbol, the Greek letter ϕ, which happens to equal 1.6180339887, approximately.  “Approximately?”  Mr. Spock.”  “I try to be precise, Captain.”

Figure 2 – The ratio of the width to the height of the Parthenon is the golden ratio phi. Original image from the Wikicommons and is by Eusebius (Guillaume Piolle)(own work).

Now before we go off on any tangents, take a look at Figure 1 again.  You see that the line b is almost a third of a+b.  Remember the “golden rule of thirds.”  If you do a little calculation you realize that instead of being 1/3 which is approximately 0.33, the fraction is actually approximately 0.38.  And it is this division of the image that we are really supposed according to the Greeks, or the imagined Greeks, to be striving for n order to attain both geometric and aesthetic perfection.

So now take a look a Figure 2, which shows the Parthenon in Athens, what did the architects Temple of the Goddess Athena choose the ratio of the width to the height to be.  Yes, you guessed it ϕ!  Perfection in the Goddess is here symbolized by perfection in the geometry of the building.

Figure 3 – The Fibonnaci spiral from the Wikicommons by Dicklyon and in the public domain.

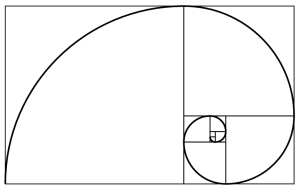
Finally, recognize that one of the key points of the construction in Figure 1, is that the placement of a line a distance a from the start of the width create a second and rotated “golden rectangle.  This construction can be done on paper with a simple drawing compass.  This process can be repeated over and over an infinite number of times each step creating a smaller and smaller “golden rectangle.”  If you look at Figure 3, you can see how this process defines a spiral, called the Fibonnaci spiral (for the mathematicians I apologize for not going into the subtle differences between the Fibonnacci spiral and the Golden spiral.”).  This is very cool!  And cooler still is the fact that this spiral is the basis for a large numbers of forms in the animal world including the ram’s horn and the spiral of ancient ammonites as well as the modern chambered Nautilus.  We find all of these to be objects of great beauty.  So therein lies the basis of the concept that this ratio is fundamental to the concept of beauty and to be emulated in the division of an image.