Suppose that you look at a point of light with your camera, what do you see? This is a trick question; so the answer isn’t a point of light. If you expand the image enough the point of light appears fuzzy. This is a property of all lenses. No lens can focus a point to a point. Instead the point gets fuzzed out. In fact it gets fuzzed out in all three dimensions. The shape of the fuzzy light is called the “point spread function” or PSF.
Figure 1 – How a point of light appears in a camera – The Airy Disk
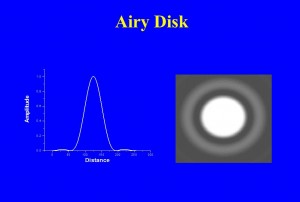
In Figure 1, I show what this point should look like on the right and an intensity scan through it on the left. You will, of course, see that it isn’t quite just a fuzzy point. Rather, there is a ring (of about 2% peak intensity) around the fuzzy center. In fact if we had enough dynamic range to display it, we would see that there are an infinite number of concentric rings, each progressively fainter than the last. This pattern is referred to as the Airy disk after the nineteenth century physicist-astronomer, Sir George Biddell Airy (see Figure 2). Those of you familiar with optics will immediate recognize that the Airy disk, because of the concentric rings, must be some kind of interference phenomenon. For now, let’s just accept it as an experimental fact. This is what we see in an optical imaging system from a point of light. For those of you interested in a complete explanation, I refer you to Arnold Sommerfeld’s excellent work on Optics and my own, more modest, paper in Digital Microscopy.
Figure 2 – Sir George Biddell Airy (1801-1892)
Now, you might ask, why blow things up so much? Why not confine the Airy disk to a single pixel. Then it would appear effectively as a point in the image. If you do this you allow the image to be pixel limited in its resolution and you do not get as much resolution as you possible can out of your optics.
Another important question, why do we care how a point behaves in an image. The answer to that takes us back to the question of a pixelated world. Every scene or image consists of a set or array of points. Therefore, if we know how the camera alters a point we will then know how it alters every scene that we can look at. I like to say that the image is the transform, by the camera, via its point spread function, of reality or the scene. This is not just a philosophical point. If we know the point spread function there are mathematical methods of reversing the fuzzing, of making the image more accurately descriptive of the true scene. This is what the various image sharpening methods used in your camera or image processing software attempt to do.
Figure 3 – Resolution in terms of overlapping Airy disks
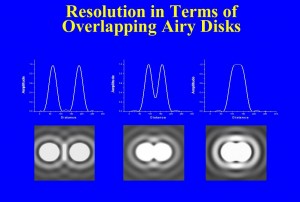
You will remember that we described how in order to see a bright spot located at a pixel and distinguish it from a second bright spot at another pixel, there had to be a darker pixel in between. The question of resolution can be described in very similar terms. If we have two points, each converted by the camera to an Airy disk, how close can they get before we cannot figure out if we are looking at one or two spots? Take a look at Figure 3. You can see that the closer the points get to one another the smaller the dip in intensity in between them. Any detector, your eye or the camera’s sensor, has some limit in its ability to see that dip. This is what defines resolution. In the nineteenth century, Lord Rayleigh defined resolution, somewhat arbitrarily, as being when the center of the second Airy disk falls on the first ring of the first Airy disk. This corresponds to approximately a 20% dip in between, and this was found to be just about what the eye could do in a telescope.
For a camera, Rayleigh’s criterion can be written as:
(separation on the image sensor)=1.22 X (wavelength of light)X(f-number).
So let’s see , if we have light of 0.5 microns (green) light and are using a f-number of 8, the resolution will be about 4 microns. We have already seen in our discussion about lenses and magnification, how to translate this to resolution size for an object at some distance.
(separation at the object) =(separation on the image sensor) / Magnification,
where,
Magnification = (focal length)/(distance to the object).
I’m trying very hard to limit the number of equations in this blog. However, the equation adds one very important point, namely that resolution is inversely related to f-number. The higher the f-number, the larger the separation distance, which means that we have less resolution. How’s that for counter-intuitive! F-number improves your depth of focus at the price of weakening image sharpness.