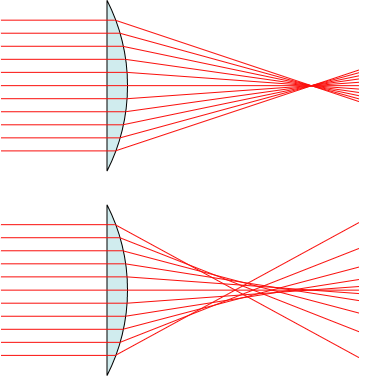
Figure 1 – Spherical aberration, (top) an ideal lens, (bottom) a lens with spherical aberation. From the Wikimedia Commons by Mglg and in the public domain under creative commons license.

I know that I have spent a lot of time discussing the issue of image sharpness or resolution.  It is a personal obsession.  Still if you read some of my posts on how a camera works, you may wonder why you can’t just stick a big honking magnifying glass in front of your camera, perhaps add your own toilet paper role to make it light tight, and call it a day.  Or, to put this question differently and to the point, why do we need to spend so many $$$ to get a good camera lens?  The answer to this question ultimately is that you need to correct for lens aberrations.  That’s where all the dollars go, and the first of these to consider is spherical aberration.

Back on September 16, 2012 we talked about Snell’s Law, which describes how light is bent as it moves from one medium, say air with its low index of refraction, into glass with its higher index of refraction, or vice versa.  That, friends, is really all you need to figure out what any lens, regardless of how complex its shape is, will do with light.  There are many computer programs, called ray tracing programs, that can do this for you, including one with the unlikely name of “FRED” that will do this for you, or rather for the optical engineers, who are designing all these wonderful lenses for us.

Figure 2 – A point source as imaged by a system with negative (top), zero (centre), and positive (bottom) spherical aberration. Images to the left are defocused toward the inside, images on the right toward the outside. From the Wikimedia Commons and released into the public domain by mdf.

Suppose, as shown in Figure 1, we consider what will happen to light coming in from far away, aka infinity.  The top panel shows a perfect lens, where all of the rays come to a point focus.  In the bottom panel a ray tracing program has been used to apply Snell’s law of refraction to each ray, taking into account the shape of the lens.  As an aside this lens has one planer surface and one convex surface.  Hence, it is called a plano-convex lens.  What you see happens is that the further off center (the center line is called the optical axis) the ray is the closer to the lens it is focused.  As a result the net affect at the image plane, where the film or camera sensor lies, is that the image gets blurred.

As an aside, the condition shown in Figure 1 is referred to as positive spherical aberration.  The off optical axis rays are bent too much.  With different shaped lenes you can get negative spherical aberration, where the off optical axis rays are bent too little and come to a focus to the right of the image plane.

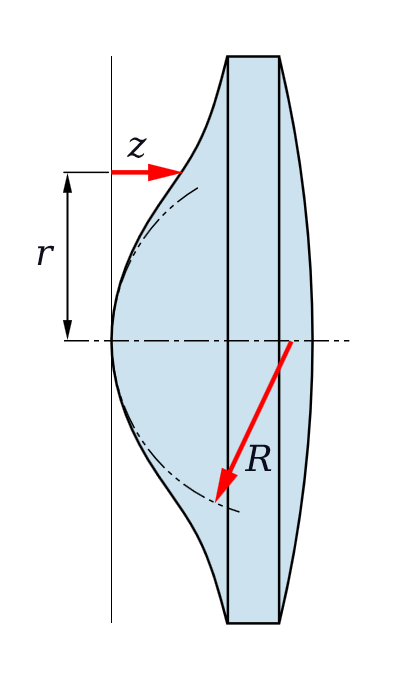
Figure3 – Example of an aspherical lens shape. From the Wikimedia Commons, originally uploaded by Pfeilhöhe and in the public domain under creative commons license.

Take a look at Figure 2, which looks at what happens to a point source of light.  Remember that we are interested in points because and image is composed of an infinite number of points – que Seurat Seurat. Here a point source of light is imaged by a system with negative (top), zero (center), and positive (bottom) spherical aberration. Images to the left are defocused toward the inside, images on the right toward the outside.  The blurring of the system due of spherical aberration is clearly seen here.

This raises the question whether you can design a lens to eliminate spherical aberration, that is to be “aspherical?”  The answer is that yes you can, at least for a single wavelength or color.  And happily you can use these same ray tracing programs to design the lens shape and surface for you.  Figure 3 shows an example of an aspherical lens.  You may have seen such shapes before.  This kind of complex aspheric shape is what is used in eyeglasses to correct for spherical aberration.

There are other ways to correct for spherical aberration. One is to use multiple lenses with compensation spherical aberration.  Another is to make the lens of variable or graded index of refraction, by depositing some dopant* into the lens that alters the local index of refraction.  Such a lens is called a GRIN lens for graded index (of refraction) lens.  All of this, I hope, is starting to sound expensive, and we have only corrected for one of many types of lens aberration.

* Dopant is a fancy science word for something added in a small amount.  For instance suppose you made a lens out of calcium carbonate (calcite), you might want to dope it with small amounts, a few percent by weight, of magnesium carbonate.